자료 구조란?
자료 구조는 기존의 컴퓨터 메모리를 보다 더 효율적으로 사용 및 관리하기 위해 새로 정의하는 구조체로서 컴퓨터 메모리에 정보를 각기 다른 방법으로 저장할 수 있도록 해준다. 대표적으로 배열, 리스트, 해시, 세트 등이 있다.
연결리스트란?
각 인덱스 값이 메모리상 연이어 저장되어있는 정적인(static) 자료구조의 배열과 달리 연결리스트는 동적인(dynamic) 자료구조로 각 노드(Node)들이 메모리상의 여러 군데 나뉘어 있는데, 각 노드에서 자신의 값뿐만 아니라 다음 노드 값의 주소(포인터)도 저장하고 있어 배열과 동일하게 값을 연이어 읽을 수 있다. 이때 마지막 노드는 다음 값이 없으므로 NULL을 다음 값의 주소로 저장한다.
연결리스트의 시간복잡도
크기가 변경될 경우 배열은 메모리 자체를 재할당하고 모든 값을 복사해야 하므로 속도가 느리지만 연결리스트는 중간에 데이터를 추가하거나 삭제하더라도 전체의 인덱스가 한 칸씩 뒤로 밀리거나 당겨지는 일이 없다. 또한 기존의 값을 모두 옮기지 않아도 리스트에 동적으로 데이터를 추가할 수 있으며 배열 보다 속도가 빠르다. 따라서 데이터의 추가나 삭제 작업이 많은 작업의 경우에는 연결 리스트를 사용하는 것이 좋다.
하지만 연결리스트는 값들이 서로 떨어져 있으므로 대괄호 [ ](인덱스 접근)를 사용할 수 없어서 배열처럼 임의의 접근이 불가능하며 값뿐만 아니라 다음 값의 주소(포인터)도 저장하므로 2배의 메모리가 필요하다. 따라서 연결 리스트의 크기가 n 일때 특정 값을 찾기 위한 검색 시간은 O(n)이지만 정렬되어 있는 배열의 경우 임의 접근이 가능하기 때문에 이진 검색을 이용하면 특정 값을 찾기 위해 O(log n)의 검색 시간이 소요 된다.(정렬되어 있지 않다면 배열 역시 O(N)의 시간 복잡도를 가진다.)
데이터 접근 또는 탐색
| 구분 | 배열 | 연결리스트 | |
| 특정 데이터 접근 | O(1), 인덱스를 통한 빠른 접근 | 순차 탐색 O(N) | |
| 특정 데이터 탐색 | 정렬 시 이진 탐색 O(log N), 정렬이 안 된 경우 선형 탐색 O(N) |
||
데이터 추가 및 삭제
| 배열 | 추가하려는 데이터 위치가 맨 뒤 이전 | O(N), 뒤에 있는 데이터 한 칸씩 뒤로 미뤄야 함 | ||
| 추가하려는 데이터 위치가 맨 뒤, 공간 여유 O | O(1) | |||
| 연결리스트 | 추가하려는 데이터 위치가 맨 앞 | O(1) | ||
| 추가하려는 데이터 위치가 맨 앞 이후 | O(N), 추가하려는 위치까지 탐색 | |||
연결리스트 구현해보기(feat. C언어)
1. node 구조체(연결리스트) 정의
연결리스트는 아래 코드와 같이 간단한 node 구조체로 정의할 수 있다. struct 뒤 node는 이 구조체의 이름으로 생략 가능하며 이때 자료구조 초기화 시에는 중괄호 뒤에 나오는 구조체의 별칭이 사용된다. 또한 node형 포인터 변수 list를 정의했다. 현재 이 포인터는 아무것도 가리키고 있지 않기 때문에 NULL로 초기화했다.
※ 참고 : node는 직사각형으로 나타낼 수 있는 메모리 덩어리를 의미한다.
typedef struct node
{
int number; // 정수형 변수 number: 1, 2, 3
struct node *next; // node형 포인터 변수 next는 다음 값의 주소를 저장하기 위함
} node;
int main(void)
{
node *list = NULL;
}
1. node 구조체(연결리스트) 도식화

2. node 메모리 할당
malloc 함수로 node형 크기의 메모리를 node형 포인터 변수 n에 할당했다. 이때 node형 크기는 정확하게 알 수 없다. 이후 n이 NULL인지 아닌지 확인되기 전까지 n을 건드리면 안되므로 if문 NULL 체크를 해주었다. 이후 n의 number 필드에 2의 값을 저장했다. 이때 n->number는 (*n).numer와 동일한 의미이다. 이는 n* 즉, n이 가리키는 node의 number 필드에 접근하여 2의 값을 할당하는 것을 의미한다. 이처럼 연결리스트는 배열의 인덱싱과 상당히 구분된다. 마지막으로 n 다음으로 정의된 node는 없으므로 NULL로 초기화했다.
node *n = malloc(sizeof(node));
if (n == NULL)
{
return 1;
}
n->number = 2;
n->next = NULL;
2. node 구조체(연결리스트) 도식화

3. 앞서 할당한 node 메모리를 node 구조체에 연결
list에 방금 할당된 메모리 덩어리 n의 주소를 대입했다. 이때 list가 첫 번째 node라면 n은 두 번째 node이다.
list = n;
3. node 구조체(연결리스트) 도식화

4. node 메모리 추가 할당 및 연결
다른 node를 더 연결하기 위해 n에 새로운 메모리(4 값의 node)를 다시 할당하고 이를 2 값을 가진 node와 연결했다.
n = malloc(sizeof(node));
if (n == NULL)
{
return 1;
}
n->number = 4;
n->next = NULL;
list->next = n;
4. node 구조체(연결리스트) 도식화

5. node 메모리 추가 할당 및 연결(반복)
다시 한 번 n 포인터에 새로운 메모리를 할당하고 number과 next의 값을 저장했다. 현재 list는 2 값의 node를 가리키고, 이는 또 4 값의 node와 연결되어 있다. 따라서 5 값의 node를 더 연결하기 위해 list 다음 node(list->next, 2 값의 node)의 다음 node(list->next->next, 4 값의 node)에 5 값의 node 메모리 주소를 저장했다.
n = malloc(sizeof(node));
if (n == NULL)
{
return 1;
}
n->number = 5;
n->next = NULL;
list->next->next = n;
이처럼 node를 추가적으로 할당하고 구조체와 연결하는 반복적인 작업을 처리하기 위해서는 다음과 같은 코드를 작성해 볼 수 있다.
node *tmp = list;
while (tmp->next != NULL)
{
tmp = tmp->next;
}
tmp->next = n;
5. node 구조체(연결리스트) 도식화

6. node 구조체 중간에 node 추가하기
우선 중간에 추가할 1 값의 node 메모리를 추가할당 했다.
n = malloc(sizeof(node));
if (n == NULL)
{
return 1;
}
n->number = 1;
n->next = NULL;
6-1. node 구조체(연결리스트) 도식화

이후 list가 가리키는 node와 같은 곳을 해당 노드(앞서 새롭게 할당된 1 값의 노드)가 가리키도록 했다.
n->next = list;
6-2. node 구조체(연결리스트) 도식화

list가 해당 노드(앞서 새롭게 할당된 1 값의 노드)를 가리키도록 했다.
list = n;
6-3. node 구조체(연결리스트) 도식화

위와 똑같은 방식으로 중간에 3 값의 node를 추가시킬 수 있다.
n = malloc(sizeof(node));
if (n == NULL)
{
return 1;
}
n->number = 3;
n->next = NULL;
n->next = list->next->next;
list->next->next = n;
6-4. node 구조체(연결리스트) 도식화

7. node 구조체 중간 node 삭제하기
위 구조체에서 2 값의 node를 삭제하고자 한다. 이에 앞서 2 값의 node에 대한 메모리 주소(list->next)를 별도 포인터 변수(*delNode)에 저장했다.
node *delNode = list->next
7-1. node 구조체(연결리스트) 도식화

2 값의 node에 대한 메모리 주소(list->next)를 3 값의 node에 대한 메모리 주소(delNode->next)로 변경시켰다.
list->next = delNode->next;
7-2. node 구조체(연결리스트) 도식화
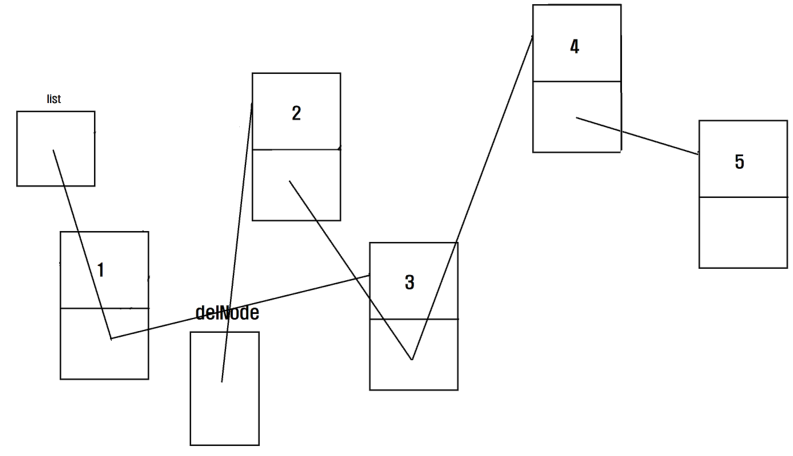
이후 2 값의 node에 대한 메모리 주소를 저장하는 delNode를 삭제했다. 2 값의 node는 어느 객체로부터 참조를 받고있지 않고 있으므로 자동으로 삭제된다.
free(delNode);
7-3. node 구조체(연결리스트) 도식화

전체 소스코드
typedef struct node
{
int number; // 정수형 변수 number: 1, 2, 3
struct node *next; // node형 포인터 변수 next는 다음 값의 주소를 저장하기 위함
} node;
int main(void)
{
node *list = NULL;
// node 구조체 끝에 node 추가하기
node *n = malloc(sizeof(node));
if (n == NULL)
{
return 1;
}
n->number = 2;
n->next = NULL;
list = n;
n = malloc(sizeof(node));
if (n == NULL)
{
return 1;
}
n->number = 4;
n->next = NULL;
list->next = n;
n = malloc(sizeof(node));
if (n == NULL)
{
return 1;
}
n->number = 5;
n->next = NULL;
list->next->next = n;
// node 구조체 중간에 node 추가하기
n = malloc(sizeof(node));
if (n == NULL)
{
return 1;
}
n->number = 1;
n->next = NULL;
n->next = list;
list = n;
n = malloc(sizeof(node));
if (n == NULL)
{
return 1;
}
n->number = 3;
n->next = NULL;
n->next = list->next->next;
list->next->next = n;
// node 구조체 중간 node 삭제하기
node *delNode = list->next
list->next = delNode->next;
free(delNode);
}
참고 자료
- 부스트코스 모두를 위한 컴퓨터 과학(CS50)
- https://m.blog.naver.com/raylee00/221944085465
'Algorithm > Basic' 카테고리의 다른 글
| 이분 탐색, Lower Bound와 Upper Bound - Java (0) | 2022.08.18 |
|---|---|
| [배열 연습] 2차원 배열 뱀 채우기 - Java (0) | 2022.08.03 |
| 소수를 판별하는 방법들 - Java (0) | 2022.06.11 |
| 유클리드 호제법을 이용한 최대공약수 구하기 - Java (0) | 2021.12.10 |
| 알고리즘의 시간 복잡도와 빅오 표기법 (0) | 2021.12.01 |