이분 탐색이란?
우선 탐색이란 자료구조, 그래프 등에서 특정한 데이터를 찾는 것을 말한다. 대표적인 탐색 방법으로 '순차 탐색'이 있는데, 이는 어떤 자료구조에서 특정 데이터를 찾기 위해 첫 번째 원소부터 마지막 원소까지 차례대로 확인하는 방법으로 가장 정직한 탐색 방법이다.
하지만 이러한 순차 탐색의 시간 복잡도는 O(N)으로 데이터가 무수히 많은 경우에는 적합하지 않다. 이러한 경우에는 어떤 탐색 방법이 유용할까? 대표적으로 '이분 탐색'이 있다. 이분 탐색은 탐색 범위를 절반씩 좁혀가며 데이터를 탐색하기 때문에 시간 복잡도가 O(logN)으로 순차 탐색 보다 훨씬 유리한 방법이다. 다만 이분 탐색의 경우 '데이터가 정렬되어 있는 경우'에만 사용할 수 있다는 특징이 있다.
이분 탐색 구현해보기
여러 개의 숫자 데이터가 산재되어 있는 리스트(List)에서 특정 숫자 데이터가 존재하는지를 검증한다고 해보자. 만일 ArrayList로 구현된 리스트의 경우 conatins 메서드를 활용하면 간단하게 해결할 수 있지만, 이는 순차 탐색 방식으로서 첫 번째 요소부터 마지막 요소까지 차례대로 탐색하면서 해당 데이터가 존재하는지 검증한다.
List<Integer> scores = new ArrayList<>();
scores.add(5);
scores.add(2);
scores.add(3);
scores.add(1);
scores.add(6);
System.out.println(scores.contains(6)); // true
그렇다면 자바로 이분 탐색을 구현해보자. 이분 탐색 구현 방식은 재귀 함수를 이용한 방식과 반복문을 이용한 방식이 있는데, 여기서는 반복문을 이용해보겠다. 앞서 언급했듯이 이분 탐색을 위해서는 먼저 데이터가 정렬되어 있어야 한다. 이를 위해 Collections 클래스의 sort 메서드로 해당 리스트를 오름차순으로 정렬해주었다.
List<Integer> scores = new ArrayList<>();
scores.add(5);
scores.add(2);
scores.add(3);
scores.add(1);
scores.add(6);
Collections.sort(scores);
이후에는 본격적으로 이분 탐색을 시작하는데, 이분 탐색은 시작점(start)과 끝점(end) 그리고 중간점(mid) 이 세 개의 변수를 이용하여 탐색 범위를 절반씩 좁혀가면서 탐색한다. 최초 시작점(start)은 0으로, 끝점(end)은 리스트의 마지막 인덱스로 설정한 후, 두 지점의 중간점(mid)을 기준으로 데이터를 찾는데, 이때 찾으려는 데이터와 일치하면 그대로 반복문을 탈출하여 true를 반환해주면 된다.
boolean result = false;
int target = 6, find;
int start = 0, end = scores.size() - 1, mid;
while (start <= end) {
mid = (start + end) / 2;
find = scores.get(mid);
if (find == target) {
result = true;
break;
}
// ...
}
하지만 찾은 데이터가 찾으려는 데이터 보다 크다면, 찾은 데이터 이후의 데이터에 대해서는 탐색할 필요가 없으므로 끝점을 중간점 보다 1 작은 값으로 설정한후 다시 중간점을 구해 다시 탐색한다.
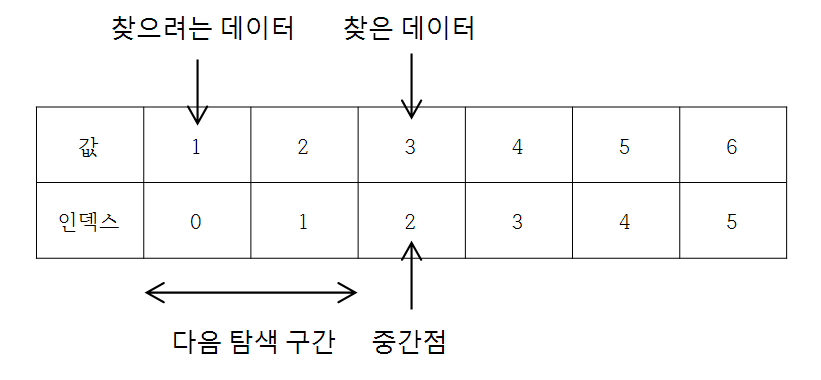
반면에 찾은 데이터가 찾으려는 데이터 보다 작다면, 찾은 데이터 이전의 데이터에 대해서는 탐색할 필요가 없으므로 시작점을 중간점 보다 1 큰 값으로 설정하여 다시 중간점을 구해 다시 탐색한다.

현재 리스트 내 데이터가 6개 있는데, 순차 탐색의 경우 최악의 경우 6번의 탐색이 필요하지만 이분 탐색의 경우 최악의 경우 3번의 탐색으로 탐색을 마칠 수 있다. 데이터가 적을 때는 이분 탐색이 빛을 발하지 못하지만 데이터가 많아질수록 기하급수적으로 탐색 시간을 절감할 수 있다.
전체 소스코드
List<Integer> scores = new ArrayList<>();
scores.add(5);
scores.add(2);
scores.add(3);
scores.add(1);
scores.add(6);
Collections.sort(scores);
boolean result = false;
int target = 6, find;
int start = 0, end = scores.size() - 1, mid;
while (start <= end) {
mid = (start + end) / 2;
find = scores.get(mid);
if (find == target) {
result = true;
break;
} else if (find > target) {
end = mid - 1;
} else { // find < target
start = mid + 1;
}
}
System.out.println(result); // true
Lower Bound와 Upper Bound
지금까지 이분 탐색을 이용하여 리스트 상에 특정 데이터가 존재하는지를 검증해주도록 했다. 하지만 단순히 특정 데이터가 존재하는지를 검증하는 게 아니라 특정 값 이상인 데이터의 개수를 요구하거나 특정 값 이하인 데이터의 개수를 요구하는 경우에는 어떻게 할까? 결론적으로 Lower Bound와 Upper Bound를 이용하면 된다.
Lower Bound
Lower Bound란 특정 값 이상인 데이터가 처음 나오는 위치를 뜻한다. 이 지점과 데이터 전체 크기를 알 수 있다면 특정 값 이상인 데이터가 몇 개인지를 알 수 있을 것이다.
Lower Bound를 찾는 이분 탐색의 경우 기존 이분 탐색과 다른 점은 끝점을 마지막 인덱스 + 1로 설정해준다는 점과 이분 탐색 조건을 시작점 <= 끝점이 아니라 시작점 < 끝점으로 설정해준다는 점 그리고 찾은 값이 찾으려는 값 보다 크거나 같은 경우 끝점을 중간점으로 초기화해준다는 점이다.
다음은 숫자 데이터로 구성된 리스트에서 4 이상의 데이터가 몇 개인지를 Lower Bound를 이용해 구한 로직이다.
List<Integer> scores = new ArrayList<>();
scores.add(5);
scores.add(2);
scores.add(3);
scores.add(1);
scores.add(6);
Collections.sort(scores);
boolean findFlag = false;
int target = 4;
int start = 0, end = scores.size(), mid;
while (start < end) {
mid = (start + end) / 2;
if (scores.get(mid) >= target) {
findFlag = true;
end = mid;
} else {
start = mid + 1;
}
}
if (!findFlag) {
System.out.println("NOT FOUND");
return;
}
System.out.println(scores.size() - end); // 2
리스트 데이터 상에는 4와 일치하는 데이터는 없지만 데이터 전체 크기에서 Lower Bound에 해당하는 인덱스 값(end)을 뺴줌으로써 결과적으로 Lower Bound인 5 그리고 6을 포함하여 총 2개의 데이터가 있다는 것을 확인할 수 있다. 참고로 찾으려는 값 보다 크거나 같은 데이터가 아무것도 없는 경우를 대비해 별도로 findFlag를 설정해주어 "NOT FOUND"를 출력시켰다.
Upper Bound
반면에 Upper Bound는 특정 값을 초과한 데이터가 처음 나오는 위치를 뜻한다. 마찬가지로 이 지점과 데이터 전체 크기를 안다면 특정 값을 초과한 데이터가 몇 개인지를 알 수 있다.
Lower Bound와 큰 차이는 없다. 단지 기존에 찾으려는 값 보다 크거나 같다는 설정에서 크다는 설정으로만 바꿔주면된다. 바로 코드로 확인해보자.
List<Integer> scores = new ArrayList<>();
scores.add(5);
scores.add(2);
scores.add(3);
scores.add(1);
scores.add(6);
Collections.sort(scores);
boolean findFlag = false;
int target = 5;
int start = 0, end = scores.size(), mid;
while (start < end) {
mid = (start + end) / 2;
if (scores.get(mid) > target) {
findFlag = true;
end = mid;
} else {
start = mid + 1;
}
}
if (!findFlag) {
System.out.println("NOT FOUND");
return;
}
System.out.println(scores.size() - end); // 1
찾으려는 데이터가 5이며, 리스트 데이터 상에 5라는 데이터가 존재하지만, 5를 초과한 데이터는 6이 유일하므로 결과값이 1임을 확인할 수 있다.
참고자료
- https://12bme.tistory.com/120
'Algorithm > Basic' 카테고리의 다른 글
| [정렬 연습] 삽입 정렬의 원리 및 구현 - Java (0) | 2022.09.07 |
|---|---|
| [정렬 연습] 버블 정렬과 선택 정렬의 원리 및 구현 - Java (0) | 2022.09.06 |
| [배열 연습] 2차원 배열 뱀 채우기 - Java (0) | 2022.08.03 |
| 소수를 판별하는 방법들 - Java (0) | 2022.06.11 |
| C언어로 연결리스트 자료 구조 구현해보기 (0) | 2022.01.09 |