삽입 정렬이란?
삽입 정렬은 주어진 데이터들을 순회하면서 특정 데이터를 적절한 위치에 삽입하는 방식으로 정렬한다. 이때 마법의 단어 '적절한'이 들어갔는데, 이 단어가 이전에 다루었던 버블 정렬과 선택 정렬과의 차이를 낳는다.
이전에 다루었던 버블 정렬과 선택 정렬의 경우, 주어진 데이터의 정렬 상태 등에 상관없이 항상 모든 요소를 순회하면서 비교하는 비효율적인 문제가 있었다. 하지만 삽입 정렬의 경우, 순회 중 특정 데이터를 삽입할 적절한 위치를 찾으면 삽입 후 기존 순회를 중단하고 다음 순회로 넘어간다. 이로써 기존 데이터의 상태가 어느정도 정렬된 상태라면, 더욱 빠른 속도로 정렬할 수 있게 된다.
그림으로 삽입 정렬의 원리 이해하기
아래와 같이 최초 정렬되지 않은 크기 10의 정수형 배열이 있다고 가정했을 때, 삽입 정렬을 통해 오름차순으로 정렬해보자.

삽입 정렬의 경우 첫 번째 데이터는 정렬이 되어 있다고 가정하고 두 번째 데이터부터 순회를 시작한다. 이때 순회의 방향은 오른쪽이 아니라 왼쪽 방향 즉, 정렬이 되어 있다고 가정한 부분들을 대상으로 하며 서로 붙어있는 데이터 2개씩 나란히 비교(버블 정렬과 유사)해나간다. 그리고 비교 결과 작은 값이 왼쪽으로 가도록 위치를 바꿔준다.(swap)
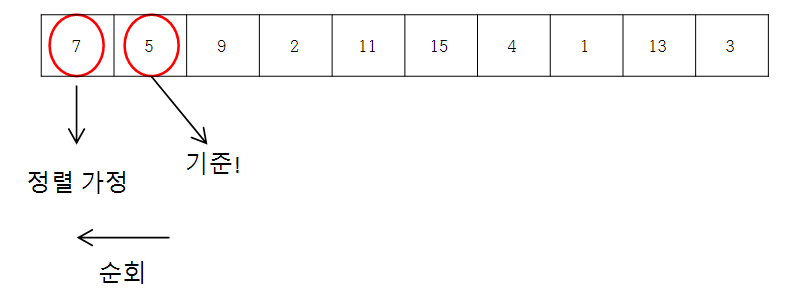

이제 첫 번째 데이터와 두 번째 데이터는 (자기들 끼리는) 정렬이 되었다고 할 수 있다. 이제 세 번째 데이터를 기준으로 다시 왼쪽으로 순회한다. 이때 중요한 점은 순회 중 비교 결과 swap이 일어나지 않으면 즉시 순회를 중단한다는 점이다. 앞서 첫 번째 데이터와 두 번째 데이터는 정렬이 되어 있기 때문에 굳이 끝까지 순회할 필요가 없는 것이다.

이제 첫 번째 데이터 ~ 세 번째 데이터는 정렬이 되었다고 할 수 있으며 네 번째 데이터를 기준으로 앞선 작업을 반복해준다. 네 번째 데이터는 3번의 swap을 거쳐 맨 앞에 삽입된다.

최종적으로 마지막 데이터를 기준으로 순회하는 작업을 마칠 때까지 앞선 작업을 반복해준다.

이처럼 삽입 정렬은 주어진 데이터들이 왼쪽에서 오른쪽으로 차근차근 정렬된다는 것을 확인할 수 있다.

자바로 삽입 정렬 구현하기
앞선 원리를 적용해 삽입 정렬을 자바로 구현해보면 다음과 같다.
public class InsertionSort {
public static void insertionSort(int[] array) {
for (int i = 1; i < array.length; i++) {
for (int j = i; j > 0; j--) {
if (array[j] >= array[j - 1]) {
break;
}
swap(array, j, j - 1);
}
}
}
private static void swap(int[] array, int i, int minIndex) {
int temp = array[i];
array[i] = array[minIndex];
array[minIndex] = temp;
}
}
재귀 함수를 이용해서도 삽입 정렬을 구현할 수 있다.
public class InsertionSort {
public static void recursiveInsertionSort(int[] array) {
recursiveInsertionSort(array, 1);
}
private static void recursiveInsertionSort(int[] array, int i) {
if (i < array.length) {
for (int j = i; j > 0; j--) {
if (array[j] >= array[j - 1]) {
break;
}
swap(array, j, j - 1);
}
recursiveInsertionSort(array, i + 1);
}
}
private static void swap(int[] array, int i, int minIndex) {
int temp = array[i];
array[i] = array[minIndex];
array[minIndex] = temp;
}
}
삽입 정렬의 성능
삽입 정렬은 주어진 데이터의 크기가 N이라고 할 때, 주어진 데이터들을 N - 1번 순회하며, 순회할 때마다 순회할 요소가 하나씩 늘어 총 연산 횟수는 1 + 2 + 3 + ... + (N - 3) + (N - 2) + (N - 1) 이다. 이를 수식으로 나타내면 (N - 1) * N / 2 로 나타낼 수 있는데, 이를 빅오 표기법으로 나타내면 O(N^2)으로 나타낼 수 있다.
여기까지는 이전에 다루었던 버블 정렬과 선택 정렬과 별 다를 바가 없어보인다. 하지만 앞서 잠시 언급했던 '적절한' 위치에 데이터를 삽입하는 순간 기존 순회 작업을 중단하고 다음 순회 작업으로 넘어가기 때문에 기존에 데이터들이 어느정도 정렬되어 있는 상태라면 훨씬 빠르게 동작할 수 있다. 최선의 경우엔 O(N)의 시간 복잡도를 가진다.
5만개의 정렬된 정수 데이터를 버블 정렬, 선택 정렬, 삽입 정렬로 각각 정렬했을 때 소요되는 시간은 다음과 같았다.
int[] array1 = new int[50000];
for (int i = 0; i < 50000; i++) {
array1[i] = i;
}

완전히 정렬된 데이터를 삽입 정렬로 정렬을 시도하는 경우엔 기존 버블 정렬과 선택 정렬과 비교해서 압도적인 성능을 보여주었다.
이번엔 3만개의 무작위 정수 데이터로 실행 시간을 측정해보았다.
int[] array2 = new int[30000];
Random random = new Random(30000);
for (int i = 0; i < 30000; i++) {
array2[i] = random.nextInt(1000);
}

확실히 정렬된 데이터를 삽입 정렬할 때보다는 무작위 데이터를 삽입 정렬로 하니 확연히 실행 시간이 증가했다. 그럼에도 불구하고 항상 모든 데이터를 순회하지 않는다는 점에서 버블 정렬과 선택 정렬에 비하면 실행 시간 측면에서 훨씬 효율적인 알고리즘이라고 볼 수 있다.
참고자료
- 한빛 미디어 출판 "이것이 취업을 위한 코딩테스트다"
'Algorithm > Basic' 카테고리의 다른 글
| [정렬 연습] 병합 정렬의 원리 및 구현 - Java (0) | 2022.09.11 |
|---|---|
| [정렬 연습] 퀵 정렬의 원리 및 구현 - Java (2) | 2022.09.10 |
| [정렬 연습] 버블 정렬과 선택 정렬의 원리 및 구현 - Java (0) | 2022.09.06 |
| 이분 탐색, Lower Bound와 Upper Bound - Java (0) | 2022.08.18 |
| [배열 연습] 2차원 배열 뱀 채우기 - Java (0) | 2022.08.03 |