뱀 채우기?
2차원 배열을 채우는데에는 여러가지 방법들이 존재한다. 예를 들면 '순서대로 채우기', '지그재그 채우기', '빗금 채우기', '달팽이 채우기' 등이 있다. 이러한 2차원 배열 채우기의 다양한 방법들은 알고리즘 문제 풀이 사이트 '코드업'에서 연습해볼 수 있다.
문제집 / 기초5-3. 2차원 배열
www.codeup.kr
참고로 달팽이 채우기 문제에 대한 풀이는 다음 글을 참고해볼 수 있다.
[코드업 - 1484] 2차원 배열 달팽이 채우기 4-1 - Java
문제 설명 [기초-배열연습] 2차원 배열 달팽이 채우기 4-1 다음과 같은 n*m 배열 구조를 출력해보자. 입력이 3 4인 경우 다음과 같이 출력한다. 1 2 3 4 10 11 12 5 9 8 7 6 입력이 4 5인 경우는 다음과 같이
ikjo.tistory.com
하지만 최근 코딩테스트에서 앞선 방법들과 유사하지만 다소 다른 문제가 출제된 적이 있었는데, 예를 들면 자연수 n이 주어지면 n * n 배열에 대해서 다음과 같은 흐름으로 각 요소를 채우는 문제였다.

사실 이러한 배열 채우기 방식에 대한 정확한 명칭을 짓기 어려워 나름대로 뱀이 이동하는 모습과 같아 '뱀 채우기'로 명명해보았다. 다른 좋은 이름도 있겠지만 우선 이번 글에서는 '뱀 채우기'라는 이름을 사용하고자 한다.
접근 방법?
사실 배열 채우기라는 문제 자체는 난이도가 그리 높은 편은 아니다. 배열 채우기는 결국 for 문과 if 문을 적절하게 잘 사용하기만 한다면 문제를 해결하는데 큰 어려움은 없다. 하지만 각각의 방법대로 나름의 규칙성이 존재하는데 이것을 제대로 파악해야한다.
그렇다면 '뱀 채우기'의 규칙성을 살펴 보자.
n = 1이라면 생각할 필요도 없이 (1, 1) 좌표의 요소에 1을 할당하면 끝이다.
n = 2일 때를 생각해보자. (1, 1) → (1, 2) → (2, 2) → (2, 1) 순으로 좌표가 바뀌면서 숫자를 채워나간다. 방향으로 따지면 RIGHT → DOWN → LEFT와 같다. 이것만 봐서는 규칙성을 파악하기 힘드니 n = 3일 때를 확인해보자.
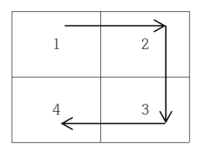
n = 3일 때의 좌표 흐름은 다음과 같다. 앞서 배열을 채운 이후에 방향의 흐름을 나타내면 DOWN → RIGHT → RIGHT → UP → UP와 같다. 아직까진 n = 2일 때의 흐름과의 규칙성을 찾기 힘들다.
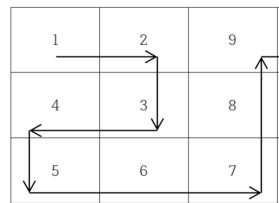
n = 4일 때의 좌표 흐름은 다음과 같다. 마찬가지로 앞서 배열을 채운 이후에 방향의 흐름을 나타내면 RIGHT → DOWN → DOWN → DOWN → LEFT → LEFT → LEFT와 같다. 개인적으로는 이 부분에서 n = 2인 경우와의 규칙성을 느낄 수 있었다. 첫 시작 부분은 RIGHT로 시작했으며 이후 DOWN과 LEFT가 일어났는데 횟수만 다를 뿐이다.

마지막으로 n = 5일 때의 좌표 흐름도 확인해보자. 앞서 배열을 채운 이후에 방향의 흐름을 나타내면 DOWN → RIGHT → RIGHT → RIGHT → RIGHT → UP → UP → UP → UP와 같다. 뭔가 익숙한 흐름인가 했더니 n = 3인 경우와 매우 흡사하다. 첫 시작 부분이 DOWN으로 시작하며 이후 RIGHT와 UP이 횟수만 다를 뿐이었다.
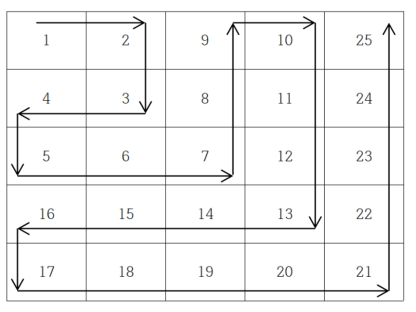
지금까지의 단서들을 바탕으로 뱀 채우기의 규칙성을 다음과 같이 정의내릴 수 있다.
1. n이 짝수 일 때의 흐름도 RIGHT → DOWN * (1, 3, 5, ...) → LEFT * (1, 3, 5, ...)
2. n이 홀수 일 때의 흐름도 DOWN → RIGHT * (0, 2, 4, ...) → UP * (0, 2, 4, ...)
직접 구현해보자!
이제 규칙성을 발견했으니, 직접 구현을 해보자.
우선 n을 입력받고 n * n 2차원 배열을 선언해준다.
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int[][] room = new int[n][n];
int x = 0 , y = 0;
room[x][y] = 1;
개인적으로 n = 1인 경우는 매우 단순하므로 직접 선언해주도록 했다. 이제 n = 2 이상인 경우를 고려해주면된다.
여기서 n 값에 따라 일종의 규칙성이 있으니, for 문을 통해 2 ~ n 순으로 순회해주도록 했다. 이때 각 값이 짝수인지 홀수인지에 따라 별도 if 문을 통해 분기처리하였으며, 시작 값과 끝 값은 다음과 같이 거듭 제곱 수로 정의해볼 수 있다.
for (int i = 2; i <= n; i++) {
int start = (int) Math.pow(i - 1, 2) + 1;
int end = (int) Math.pow(i, 2);
int half = (int) Math.ceil( (double) (end + start + 1) / 2);
if (i % 2 == 0) {
// TODO
} else {
// TODO
}
}
앞서 'DOWN 및 LEFT' 또는 'RIGHT 및 UP'이 여러번 반복되는데, 시작점에서 + 1 지점과 끝점 구간의 절반의 길이만큼 반복되는 것을 확인할 수 있었다. 이때 half 변수의 역할은 각각의 방향대로 반반씩 이동하게 하기 위함이다.
최종적으로 각 분기문 내에 흐름을 앞서 다루었던 규칙성대로 나타내보면 다음과 같다.
if (i % 2 == 0) {
y++;
room[x][y] = start;
for (int j = start + 1; j < half; j++) {
x++;
room[x][y] = j;
}
for (int j = half; j <= end; j++) {
y--;
room[x][y] = j;
}
} else {
x++;
room[x][y] = start;
for (int j = start + 1; j < half; j++) {
y++;
room[x][y] = j;
}
for (int j = half; j <= end; j++) {
x--;
room[x][y] = j;
}
}
다 구현했으면 '뱀 채우기'의 동작 결과를 확인해보자.
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
System.out.printf("%d ", room[i][j]);
}
System.out.println();
}
전체 소스 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int[][] room = new int[n][n];
int x = 0 , y = 0;
room[x][y] = 1;
for (int i = 2; i <= n; i++) {
int start = (int) Math.pow(i - 1, 2) + 1;
int end = (int) Math.pow(i, 2);
int half = (int) Math.ceil( (double) (end + start + 1) / 2);
if (i % 2 == 0) {
y++;
room[x][y] = start;
for (int j = start + 1; j < half; j++) {
x++;
room[x][y] = j;
}
for (int j = half; j <= end; j++) {
y--;
room[x][y] = j;
}
} else {
x++;
room[x][y] = start;
for (int j = start + 1; j < half; j++) {
y++;
room[x][y] = j;
}
for (int j = half; j <= end; j++) {
x--;
room[x][y] = j;
}
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
System.out.printf("%d ", room[i][j]);
}
System.out.println();
}
}
}
'Algorithm > Basic' 카테고리의 다른 글
| [정렬 연습] 버블 정렬과 선택 정렬의 원리 및 구현 - Java (0) | 2022.09.06 |
|---|---|
| 이분 탐색, Lower Bound와 Upper Bound - Java (0) | 2022.08.18 |
| 소수를 판별하는 방법들 - Java (0) | 2022.06.11 |
| C언어로 연결리스트 자료 구조 구현해보기 (0) | 2022.01.09 |
| 유클리드 호제법을 이용한 최대공약수 구하기 - Java (0) | 2021.12.10 |