문제 설명
25682번: 체스판 다시 칠하기 2
첫째 줄에 정수 N, M, K가 주어진다. 둘째 줄부터 N개의 줄에는 보드의 각 행의 상태가 주어진다. B는 검은색이며, W는 흰색이다.
www.acmicpc.net
접근 방법
5개월 전 체스판 다시 칠하기(백준 - 1018) 라는 문제를 푼 적이 있었는데, 최근 체스판 다시 칠하기 2(백준 - 25682) 문제가 새롭게 등장했습니다.
[백준 - 1018] 체스판 다시 칠하기 - Java
문제 설명 1018번: 체스판 다시 칠하기 첫째 줄에 N과 M이 주어진다. N과 M은 8보다 크거나 같고, 50보다 작거나 같은 자연수이다. 둘째 줄부터 N개의 줄에는 보드의 각 행의 상태가 주어진다. B는 검
ikjo.tistory.com
앞서 풀었던 체스판 다시 칠하기(백준 - 1018)의 경우는 주어진 M * N 크기의 보드로부터 8 * 8 크기 만큼만 잘라 체스판을 구하면됐으므로, 로직 편의상 2 종류의 8 * 8 크기의 체스판을 선언한 후 M * N 크기의 보드를 일일이 순회하면서 일치하는지 검증해주도록 했었습니다.
위 문제에서는 N과 M의 크기가 최대 50이었기 때문에 보드를 순회하기 위한 4중 for문을 적용해도 별도의 시간 제한 이슈는 없었습니다. 하지만 이번에 새롭게 나온 체스판 다시 칠하기 2(백준 - 25682) 문제의 경우 N과 M의 크기가 최대 2000이기 때문에 4중 for문을 적용하게 되면 제한 시간 1초를 지킬 수 없게 됩니다.
따라서 이번 문제에서는 일일이 검증(브루트포스)하는 것이 아닌 누적합을 이용해 나름대로의 최적화(2중 for문)를 하였습니다.
이때 무엇을 누적합할 것인가를 생각해볼 수 있었는데, 문제에서 요구하는 것이 K * K 보드를 체스판으로 만들기 위해 다시 칠해야 하는 정사각형의 개수의 최솟값이므로, 각 칸별로 다시 칠해야하는 정사각형의 개수를 누적하여 더해주고자 했습니다.
문제에서 주어진 예제 입력 1을 기준으로 살펴보겠습니다.

우선 처음 격자가 B로 시작하는 경우에는 아래 표시된 영역에 대해 다시 칠해야 합니다.

이를 2차원 행렬 상에 누적하여 더하면 다음과 같은 결과가 나옵니다.
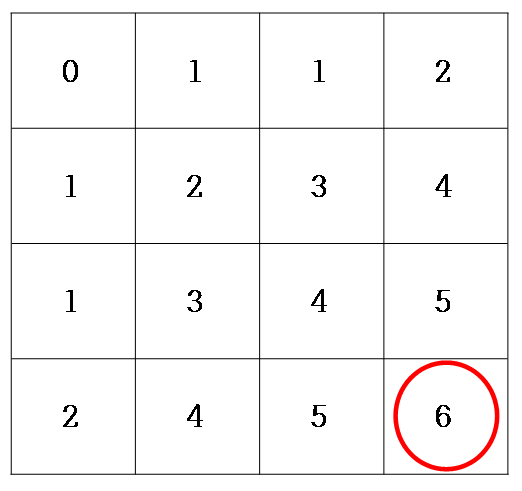
누적합의 결과로 2차원 행렬 상 가장 마지막(4, 4 지점) 원소의 값은 4 * 4 격자 상 다시 칠해야 하는 전체 개수로 나타나게 됩니다. (이때 각 요소의 값은 첫 번째 격자부터 해당 요소까지의 (직사각형 내에) 다시 칠해야 하는 전체 개수를 나타냅니다.)
이번에는 처음 격자가 W로 시작하는 경우에 대해 살펴보겠습니다.

마찬가지로 이를 2차원 행렬 상에 누적하여 더하면 다음과 같은 결과가 나오며, 누적합의 결과로 2차원 행렬 상 가장 마지막(4, 4 지점) 원소의 값은 4 * 4 격자 상 다시 칠해야 하는 전체 개수로 나타나게 됩니다.
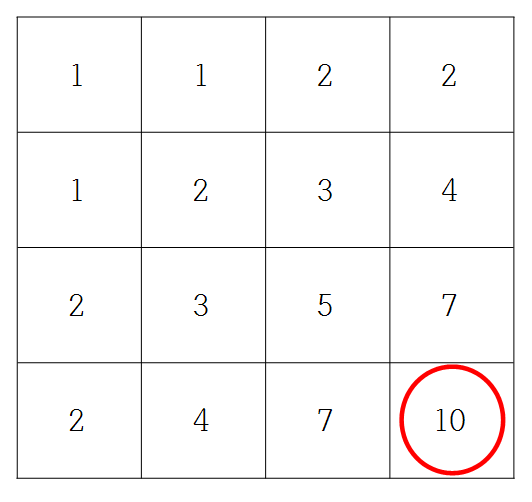
이러한 특성을 이용하면 4중 for문이 아닌 2중 for문으로 문제 요구사항을 충족시킬 수 있습니다. 앞서 처음 격자가 B로 시작하는 경우와 W로 시작하는 경우를 나누어 생각했으므로, 2개의 2차원 배열을 선언하고 위와 같이 다시 칠해야 하는 개수를 카운팅하여 누적하여 더해주도록 합니다. 이후 2중 for문으로 K * K 크기만큼의 체스판을 검증해주되 해당 체스판 내 마지막 요소의 값을 이용하여 다시 칠해야 하는 개수를 구하고 최종적으로 가장 작은 값을 취하도록 합니다. (구현 내용은 아래 소스 코드를 참고해주세요.)
소스 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
class Main {
static int[][] black, white;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken()), m = Integer.parseInt(st.nextToken()), k = Integer.parseInt(st.nextToken());
black = new int[n + 1][m + 1];
white = new int[n + 1][m + 1];
String s;
for (int i = 1; i <= n; i++) {
s = br.readLine();
for (int j = 1; j <= m; j++) {
if (s.charAt(j - 1) == 'B') {
if (check(i, j)) {
sumWhite(i, j);
} else {
sumBlack(i, j);
}
} else {
if (check(i, j)) {
sumBlack(i, j);
} else {
sumWhite(i, j);
}
}
}
}
int result = 4000000;
for (int i = 0; i <= n - k; i++) {
for (int j = 0; j <= m - k; j++) {
result = Math.min(
result,
Math.min(
black[i + k][j + k] - black[i][j + k] - black[i + k][j] + black[i][j],
white[i + k][j + k] - white[i][j + k] - white[i + k][j] + white[i][j]
)
);
}
}
System.out.println(result);
}
private static boolean check(int row, int col) {
return row % 2 == 1 && col % 2 == 1 || row % 2 == 0 && col % 2 == 0;
}
private static void sumWhite(int row, int col) {
black[row][col] = black[row - 1][col] + black[row][col - 1] - black[row - 1][col - 1];
white[row][col] = white[row - 1][col] + white[row][col - 1] - white[row - 1][col - 1] + 1;
}
private static void sumBlack(int row, int col) {
black[row][col] = black[row - 1][col] + black[row][col - 1] - black[row - 1][col - 1] + 1;
white[row][col] = white[row - 1][col] + white[row][col - 1] - white[row - 1][col - 1];
}
}
참고자료
'Algorithm > BOJ' 카테고리의 다른 글
| [백준 - 2206] 벽 부수고 이동하기 - Java (2) | 2022.09.16 |
|---|---|
| [백준 - 2110] 공유기 설치 - Java (0) | 2022.09.13 |
| [백준 - 20159] 동작 그만. 밑장 빼기냐? - Java (0) | 2022.09.13 |
| [백준 - 2263] 트리의 순회 - Java (2) | 2022.09.11 |
| [백준 - 1052] 물병 - Java (0) | 2022.09.06 |