문제 설명
접근 방법
우선 문제에서 주어진 예시를 기준으로, 정훈이가 얻을 수 있는 카드 값의 합의 경우의 수는 다음과 같습니다.
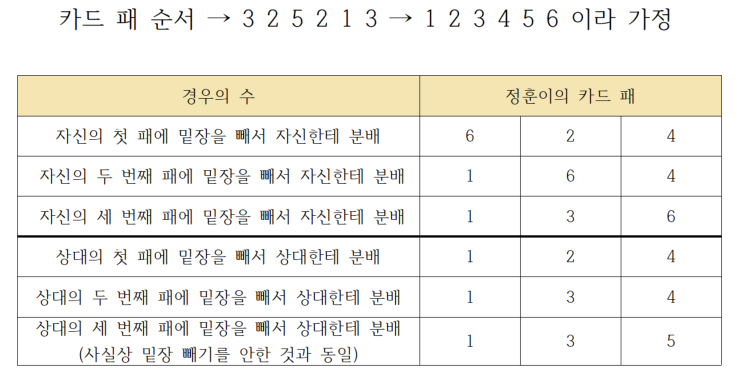
이때, 각 경우의 수를 '밑장을 빼서 자신한테 분배한 경우'와 '밑장을 빼서 상대한테 분배한 경우'로 나누어 생각해볼 수 있겠습니다.
우선 밑장을 빼서 자신한테 분배한 경우를 살펴보겠습니다.

이 경우 당연히 정훈이의 카드 패에는 밑장(카드 패 맨 마지막 순서)이 항상 포함됩니다. 그리고 1번째 및 3번째 카드와 2번째 4번째 카드가 일종의 규칙성을 나타내며 번갈아 등장하는 것 같아 보입니다.
참고로 만일 밑장 빼기를 하지 않았을 경우, 정상적으로는 1, 3, 5 번째 카드가 정훈이에게, 2, 4, 6 번째 카드가 상대에게 분배되게 됩니다. 하지만 중간에 밑장 빼기를 했기 때문에 원래대로라면 상대에게 갔어야 할 카드가 정훈이한테 오게된 것이며, 특히 밑장은 원래 상대에게 갔어야 할 카드입니다.

아무튼 위 규칙을 따져보면 정훈이가 얻을 수 있는 카드 값의 합에 대해 다음과 같은 식을 세울 수 있을 것 같습니다. 아래 식에서 0 번째 카드라 함은 값이 없는 상태인 0으로 간주해보겠습니다.

이때 특정 수들의 구간 합을 구할 때는 일일이 더해주는 것보다는 '누적합'을 이용하면 훨씬 더 적은 연산으로 처리할 수 있습니다. 따라서 최초 정훈이에게 갔어야 할 카드들의 누적 합과 상대에게 갔어야 할 카드들의 누적 합을 만들어줍니다.
int n = Integer.parseInt(br.readLine());
int[] cards = new int[n];
int half = n / 2;
int[] myCards = new int[half + 1];
int[] yourCards = new int[half + 1];
StringTokenizer st = new StringTokenizer(br.readLine());
for (int i = 0; i < n; i++) {
cards[i] = Integer.parseInt(st.nextToken());
}
for (int i = 1, me = 0, you = 1; i <= half; i++, me += 2, you += 2) {
myCards[i] = cards[me] + myCards[i - 1];
yourCards[i] = cards[you] + yourCards[i - 1];
}
이제 정훈이 카드와 상대의 카드에 대해 누적합을 구했으니, 이를 통해 앞서 정훈이가 얻을 수 있는 카드 값의 합에 대한 수식을 다음과 같이 나타낼 수 있겠습니다.
yourCards[half] - yourCards[i - 1] + myCards[i - 1]
또한 이 수식을 통해 정훈이가 밑장 빼기를 해서 자기 자신한테 분배했을 경우, 정훈이가 얻을 수 있는 카드 값의 합에 대한 최댓값을 다음과 같이 구할 수 있겠습니다.
int result = 0;
for (int i = 1; i <= half; i++) {
// 밑장을 빼서 나한테 분배하는 경우
result = Math.max(result, yourCards[half] - yourCards[i - 1] + myCards[i - 1]);
}
이번에는 밑장을 빼서 상대한테 분배한 경우를 살펴보겠습니다.

앞선 경우와 마찬가지로 자신에게 갔어야 할 카드(1, 3, 5 번째 카드)와 상대에게 갔어야 할 카드(2, 4 번째 카드)가 일종의 규칙성을 나타내며 번갈아 등장하는 것 같아 보입니다.
위 규칙을 따져보면 정훈이가 얻을 수 있는 카드 값의 합에 대해 다음과 같은 식을 세울 수 있을 것 같습니다.

이 식과 함께 앞서 구한 누적합을 통해 정훈이가 밑장을 빼서 상대한테 분배한 경우, 정훈이가 얻을 수 있는 카드 값의 합에 대한 최댓값을 다음과 같이 구할 수 있겠습니다. 이때 이전에 밑장을 빼서 자기 자신한테 분배한 경우와 함께 순회하면 되겠습니다.
int result = 0;
for (int i = 1; i <= half; i++) {
// 밑장을 빼서 나한테 분배하는 경우
result = Math.max(result, yourCards[half] - yourCards[i - 1] + myCards[i - 1]);
// 밑장을 빼서 상대한테 분배하는 경우 + 밑장을 빼지 않는 경우
result = Math.max(result, yourCards[half - 1] - yourCards[i - 1] + myCards[i]);
}
소스 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int[] cards = new int[n];
int half = n / 2;
int[] myCards = new int[half + 1];
int[] yourCards = new int[half + 1];
StringTokenizer st = new StringTokenizer(br.readLine());
for (int i = 0; i < n; i++) {
cards[i] = Integer.parseInt(st.nextToken());
}
for (int i = 1, me = 0, you = 1; i <= half; i++, me += 2, you += 2) {
myCards[i] = cards[me] + myCards[i - 1];
yourCards[i] = cards[you] + yourCards[i - 1];
}
int result = 0;
for (int i = 1; i <= half; i++) {
// 밑장을 빼서 나한테 분배하는 경우
result = Math.max(result, yourCards[half] - yourCards[i - 1] + myCards[i - 1]);
// 밑장을 빼서 상대한테 분배하는 경우 + 밑장을 빼지 않는 경우
result = Math.max(result, yourCards[half - 1] - yourCards[i - 1] + myCards[i]);
}
System.out.println(result);
}
}
참고자료
- https://www.acmicpc.net/problem/20159
'Algorithm > BOJ' 카테고리의 다른 글
| [백준 - 2206] 벽 부수고 이동하기 - Java (2) | 2022.09.16 |
|---|---|
| [백준 - 2110] 공유기 설치 - Java (0) | 2022.09.13 |
| [백준 - 2263] 트리의 순회 - Java (2) | 2022.09.11 |
| [백준 - 1052] 물병 - Java (0) | 2022.09.06 |
| [백준 - 1011] Fly me to the Alpha Centauri - Java (0) | 2022.09.06 |