문제 설명
1011번: Fly me to the Alpha Centauri
우현이는 어린 시절, 지구 외의 다른 행성에서도 인류들이 살아갈 수 있는 미래가 오리라 믿었다. 그리고 그가 지구라는 세상에 발을 내려 놓은 지 23년이 지난 지금, 세계 최연소 ASNA 우주 비행
www.acmicpc.net
접근 방법
해당 문제는 규칙성을 세워서 해결할 수 있었습니다.
우선 주어지는 x 좌표와 y 좌표 사이의 거리(y - x) 일부(1 ~ 16)에 대해 공간 이동 장치 작동 횟수(이하 '이동 횟수')의 최솟값을 일일이 구해 나타내보면 다음과 같습니다.
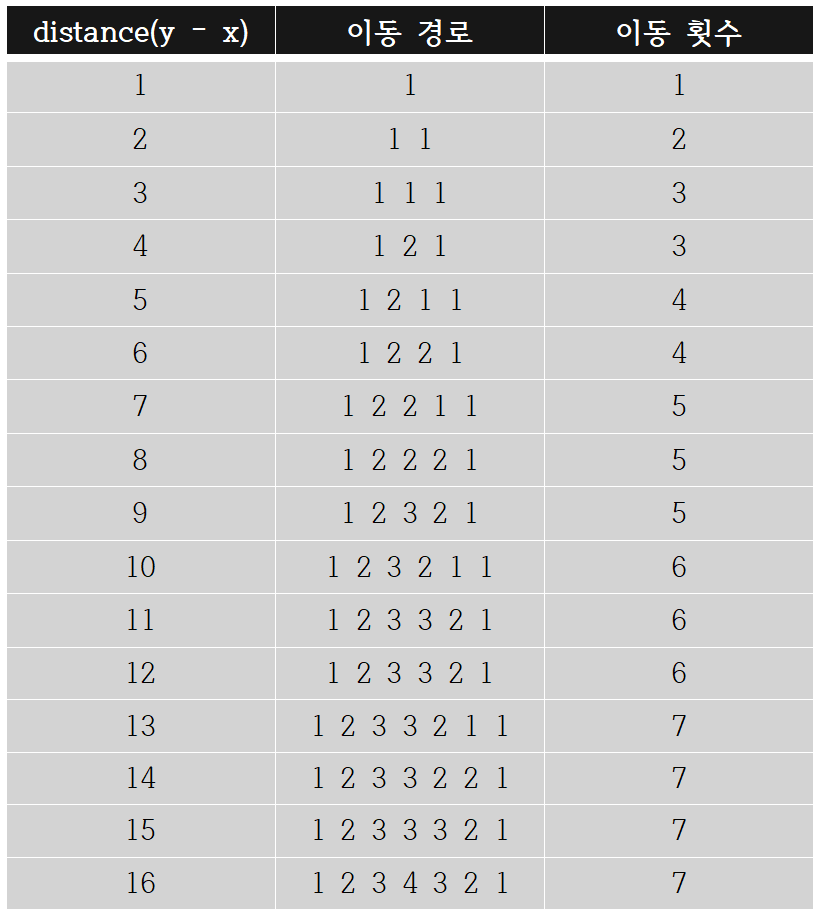
이때 이동 경로를 통해 하나 유추해볼 수 있는 것은 만일 거리(distance)의 값이 제곱수(1, 4, 9, ...)에 해당된다면, 이동 횟수는 '해당 제곱수의 제곱근' * 2 - 1 라는 점입니다.
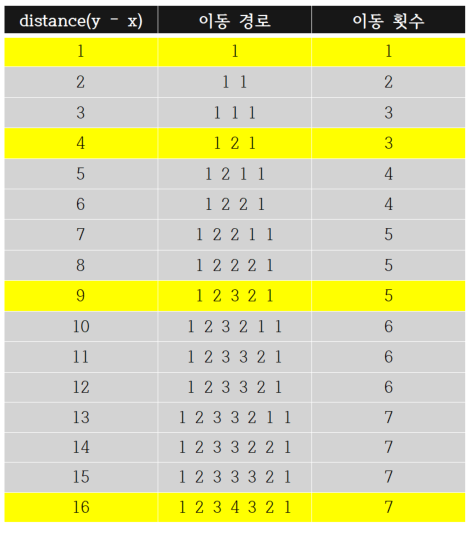

이를 코드로 나타내면 다음과 같습니다.
// ...
int distance = y - x;
double sqrtOfDistance = Math.sqrt(distance);
int integerOfSqrt = (int) sqrtOfDistance;
int countOfMove;
if (sqrtOfDistance == integerOfSqrt) {
countOfMove = integerOfSqrt * 2 - 1;
}
// ...
거리가 제곱수가 아닌 수들에 대해서도 나름대로의 규칙이 존재합니다.

우선, 제곱수인 4와 9 사이에 있는 값들을 살펴보겠습니다. 4와 9 사이 중간을 기준으로 나누어 거리가 5와 6인 수의 이동 횟수는 4의 제곱근인 2에 2를 곱한 값이며, 거리가 7과 8인 수의 이동 횟수는 4의 제곱근인 2에 2를 곱한 수에 1을 더한 값입니다.
이때 중간을 나누는 값의 기준은 자기 자신(거리) '보다 작은 제곱수'와 '보다 큰 제곱수'를 곱한 값으로 이보다 같거나 작으면 자기 자신 보다 작은 제곱수에 2를 곱한 값이 이동 횟수이며, 보다 크면 자기 자신 보다 작은 제곱수에 2를 곱한 후 1을 더한 값이 이동 횟수가 됩니다.
마찬가지로 제곱수인 9와 16 사이에 있는 값들도 살펴보면, 9와 16 사이 중간을 기준으로 나누어 거리가 10, 11, 12인 수들은 자기들 보다 작은 제곱수의 제곱근인 3에 2를 곱한 값이며, 거리가 13, 14, 15인 수들은 자기들 보다 작은 제곱수의 제곱근인 3에 2를 곱한 수에 1을 더한 값입니다.
이러한 규칙을 토대로 코드로 나타내보면 다음과 같습니다.
else { // 제곱수가 아니면
countOfMove = integerOfSqrt * 2; // 자기 자신 보다 작은 제곱수에 2를 곱한 후
if (integerOfSqrt * (integerOfSqrt + 1) < distance) { // 제곱 수 사이 중간 보다 클 경우
countOfMove += 1; // 1을 더한다
}
}
System.out.println(countOfMove); // 결과값 출력
전체 소스 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int t = Integer.parseInt(br.readLine());
for (int i = 0; i < t; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
int x = Integer.parseInt(st.nextToken()), y = Integer.parseInt(st.nextToken());
int distance = y - x;
double sqrtOfDistance = Math.sqrt(distance);
int integerOfSqrt = (int) sqrtOfDistance;
int countOfMove;
if (sqrtOfDistance == integerOfSqrt) {
countOfMove = integerOfSqrt * 2 - 1;
} else {
countOfMove = integerOfSqrt * 2;
if (integerOfSqrt * (integerOfSqrt + 1) < distance) {
countOfMove += 1;
}
}
System.out.println(countOfMove);
}
}
}
참고 자료
- https://www.acmicpc.net/problem/1011
'Algorithm > BOJ' 카테고리의 다른 글
| [백준 - 2263] 트리의 순회 - Java (2) | 2022.09.11 |
|---|---|
| [백준 - 1052] 물병 - Java (0) | 2022.09.06 |
| [백준 - 9019] DSLR - Java (0) | 2022.08.20 |
| [백준 - 1068] 트리 - Java (0) | 2022.08.17 |
| [백준 - 25332] 수들의 합 8 - Java (0) | 2022.08.11 |