문제 설명
25332번: 수들의 합 8
$A = \{1, 2, 3\}$, $B = \{1, 3, 2\}$로, 조건을 만족하는 $i, j$ 쌍은 $(1, 1), (2, 3), (1, 3)$의 세 가지이다. $A_1$ = $B_1 = 1$ $A_2 + A_3 = B_2 + B_3 = 5$ $A_1 + A_2 + A_3 = B_1 + B_2 + B_3 = 6$
www.acmicpc.net
접근 방법
해당 문제는 원티드 주관 코딩테스트 대회 2022년 2회차의 마지막 문제로서 단순하게 해결할 수 있어 보였지만, 시간 제한 등의 이슈로 다소 깐깐했었던 문제였습니다. 특히, 이 문제의 경우 백준 2015번 문제 '수들의 합 4'과 매우 밀접한 관련이 있는 문제이기에 해당 문제를 풀기 앞서 '수들의 합 4' 문제를 먼저 풀어보는 것이 많은 참고가 될 수 있습니다.
우선 문제에서 A 집합의 수열(A1, A2, A3, ... An)과 B 집합의 수열(B1, B2, B3, ... Bn)이 주어지는데, 이때 문제에서 요구하는 것은 해당 수열에서 A(i) + A(i+1) + A(i+2) + ... A(j) = B(i) + B(i+1) + B(i+2) + ... B(j)를 만족하는 쌍의 개수를 구하는 것입니다. i와 j는 양의 정수로 i는 j보다 작거나 같으며 i와 j 사이에는 연속적인 수들로 구성됩니다.
여기서 i와 j 사이가 연속적인 수로 구성되었다는 점을 통해서 '누적합'을 활용해볼 수 있겠다는 생각이 들었습니다. 두 수열간의 특정 i, j 구간 부분합에 대해서 일치 여부를 검증할 때마다 그 구간내에 수들을 일일이 더해주는 것은 매우 비효율적일 것입니다. 이때 누적합을 이용한다면 마이너스(-) 연산 한번으로 특정 구간의 부분합을 구할 수 있게 됩니다.

이를 활용하기 위해 우선 문제에서 주어진 A 수열과 B 수열에 대한 누적합을 구해주도록 합니다.
StringTokenizer st1 = new StringTokenizer(br.readLine());
StringTokenizer st2 = new StringTokenizer(br.readLine());
int[] sumA = new int[n + 1], sumB = new int[n + 1];
for (int i = 1; i <= n; i++) {
sumA[i] = Integer.parseInt(st1.nextToken()) + sumA[i - 1];
sumB[i] = Integer.parseInt(st2.nextToken()) + sumB[i - 1];
}
그 다음에 할 일은 이제 이 누적합된 배열을 활용해 각 구간별로 일치하는지 여부를 검증하는 것이겠습니다. 이때 각 수열별로 존재하는 구간의 개수는 n * (n + 1) / 2 만큼 존재하게 됩니다.

누적합을 구해놨으니, 각 구간별 합을 구하는 것은 어렵지 않은 일이고, 아래 소스 코드와 같이 2중 for문으로 정답을 구해낼 수 있어보입니다.
for (int i = 0; i < n; i++) {
a[i] = Integer.parseInt(st1.nextToken());
b[i] = Integer.parseInt(st2.nextToken());
if (a[i] == b[i]) {
result++;
}
}
// ...
for (int i = 0; i < n / 2; i++) {
for (int j = i + 2; j < n - i; j++) {
if (sumA[j] - sumA[i] == sumB[j] - sumB[i]) {
result++;
}
if (sumA[n - i] - sumA[n - j] == sumB[n - i] - sumB[n - j]) {
result++;
}
}
}
for (int i = 0; i < n / 2; i++) {
if (sumA[n - i] - sumA[i] == sumB[n - i] - sumB[i]) {
result++;
}
}

나름대로 2중 for문을 최적화해본다고 작성한 소스 코드이긴 하지만 N이 최대 20만이기에 2중 for문 적용 시 대략 100억번의 순회가 일어나므로 시간 제한 1초 이내 연산하는 것은 불가능하게 됩니다. 즉, 각 구간별로 '일일이' (선형적으로) 검증하기 위해서는 2중 반복문의 사용이 필수 불가결하므로 2중 반복문이 아닌 단일 반복문만으로도 (비선형적으로) 각 구간에 대해 검증할 수 있어야 합니다.
단순히 조건문, 반복문 등의 연산으로 탐색하는 것은 힘들기에, 빠른 탐색이 용이한 해쉬 자료구조를 활용해볼 수 있겠습니다.
이에 앞서 우리는 A 수열과 B 수열에 대한 누적합을 구했습니다. 만일 n = 5라고 가정했을 때 누적합에 대한 요소들은 아래 그림 상에서 파란색 표시 부분에 해당되겠습니다. 각각 1 ~ 1, 1 ~ 2, 1 ~ 3 등의 구간 합에 대한 현황을 나타내고 있습니다.

우선 1 ~ 1, 1 ~ 2, 1 ~ 3 등 적어도 이 구간합에 대해서는 A(i) + A(i+1) + A(i+2) + ... A(j) = B(i) + B(i+1) + B(i+2) + ... B(j)를 만족하는지 즉, a = a', b = b', c = c' ... 등을 검증하는 것은 쉬워보입니다.
for (int i = 1; i <= n; i++) {
sumA[i] = Integer.parseInt(st1.nextToken()) + sumA[i - 1];
sumB[i] = Integer.parseInt(st2.nextToken()) + sumB[i - 1];
if (sumA[i] == sumB[i]) {
result++;
}
// ...
}
위와 같이 처음 누적합을 구할 때 그 값이 같은지를 검증해주기만 하면 됩니다. 문제는 이 외의 구간들입니다.
앞서 언급했듯이 누적합의 요소들을 적절하게 활용한다면 특정 구간들에 대해 용이하게 검증할 수 있습니다. 예를 들어, 2 ~ 3 구간은 1 ~ 3 구간에서 1 ~ 1 구간을 빼면 구할 수 있고, 3 ~ 3 구간은 1 ~ 3 구간에서 1 ~ 2 구간을 빼면 구할 수 있습니다.
여기서 A 수열의 2 ~ 3 구간의 값은 c - a가 되겠고, B 수열의 2 ~3 구간의 값은 c' - a'가 되겠습니다. 따라서 c - a = c' - a' 인지를 검증해주면 되는 것입니다. 이때 c - a = c' - a 식은 c - c' = a - a' 식으로 바꿔 생각해볼 수도 있습니다.
이를 활용하여 최초 누적합을 계산해나갈 때 가장 먼저 a - a' 즉, sumA[1] - sumB[1]의 값을 해쉬 맵에 저장 및 카운팅(counting) 해놓습니다. 이때 a - a' 값의 개수는 이후 c - a = c' - a'를 만족하는 경우의 수(i, j 쌍의 개수)를 찾기 위해 사용될 수 있습니다. 앞서 c를 언급했기에 c라고 표시했지만 이는 b, d, e가 될수도 있습니다.
다시 한 번 설명하자면 a는 1 ~ 1 구간 합을 의미하고 c는 1 ~ 3 구간 합을 의미합니다. c에서 a를 뺀다는 것은 2 ~ 3 구간 합을 의미하며 이 값이 c' - a'의 값과 일치하면 문제의 A(i) + A(i+1) + A(i+2) + ... A(j) = B(i) + B(i+1) + B(i+2) + ... B(j) 조건을 만족하게 됩니다. 마찬가지로 b, d, e 각각에 대해 a를 뺀다면, 각각 2 ~ 2 구간, 2 ~ 4 구간, 2 ~ 5 구간이 되겠습니다. 이 구간들은 앞서 누적합을 구할 때 고려할 수 없었던 구간들이므로 a - a' 값을 해시에 저장하고 카운팅하는 것은 유의미하게 됩니다.
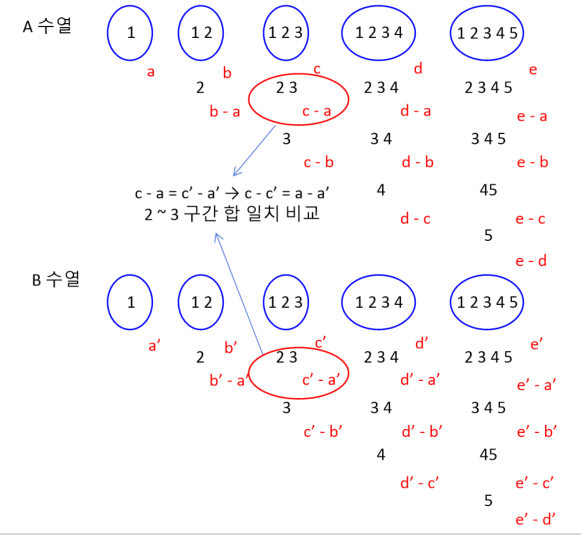
이러한 특성을 이용해 b - b'의 값도 저장 및 카운팅한다면 추후에 c - c', d - d' 등의 값을 해쉬 맵으로 검색할 때 c - b = c' - b'와 d - b = d' - b' 등의 조건을 충족하는지 검증할 수 있는 효과를 얻을 수 있습니다. 일치할 경우 문제 조건에 맞는 경우의 (i, j) 쌍이 되게 됩니다.
long result = 0;
Map<Integer, Integer> map = new HashMap<>();
for (int i = 1; i <= n; i++) {
sumA[i] = Integer.parseInt(st1.nextToken()) + sumA[i - 1];
sumB[i] = Integer.parseInt(st2.nextToken()) + sumB[i - 1];
if (sumA[i] == sumB[i]) {
result++;
}
result += map.getOrDefault(sumA[i] - sumB[i], 0);
map.put(sumA[i] - sumB[i], map.getOrDefault(sumA[i] - sumB[i], 0) + 1);
}
전체 소스 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.HashMap;
import java.util.Map;
import java.util.StringTokenizer;
class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int[] sumA = new int[n + 1], sumB = new int[n + 1];
StringTokenizer st1 = new StringTokenizer(br.readLine());
StringTokenizer st2 = new StringTokenizer(br.readLine());
long result = 0;
Map<Integer, Integer> map = new HashMap<>();
for (int i = 1; i <= n; i++) {
sumA[i] = Integer.parseInt(st1.nextToken()) + sumA[i - 1];
sumB[i] = Integer.parseInt(st2.nextToken()) + sumB[i - 1];
if (sumA[i] == sumB[i]) {
result++;
}
result += map.getOrDefault(sumA[i] - sumB[i], 0);
map.put(sumA[i] - sumB[i], map.getOrDefault(sumA[i] - sumB[i], 0) + 1);
}
System.out.println(result);
}
}
참고 자료
- https://www.acmicpc.net/problem/25332
'Algorithm > BOJ' 카테고리의 다른 글
| [백준 - 9019] DSLR - Java (0) | 2022.08.20 |
|---|---|
| [백준 - 1068] 트리 - Java (0) | 2022.08.17 |
| [백준 - 25331] Drop 7 - Java (2) | 2022.08.08 |
| [백준 - 14503] 로봇 청소기 - Java (0) | 2022.08.03 |
| [백준 - 1806] 부분합 - Java (0) | 2022.08.03 |