문제 설명
11403번: 경로 찾기
가중치 없는 방향 그래프 G가 주어졌을 때, 모든 정점 (i, j)에 대해서, i에서 j로 가는 경로가 있는지 없는지 구하는 프로그램을 작성하시오.
www.acmicpc.net
소스 코드
import java.util.Scanner;
class Main {
static int n;
static int[][] graph;
static boolean[][] visited;
public static void main(String args[]) {
Scanner sc = new Scanner(System.in);
n = Integer.parseInt(sc.nextLine());
graph = new int[n+1][n+1];
visited = new boolean[n+1][n+1];
for (int i = 1; i < n+1; i++) {
for (int j = 1; j < n+1; j++) {
graph[i][j] = sc.nextInt();
}
}
for (int i = 1; i < n+1; i++) { // 출발
for (int j = 1; j < n+1; j++) { // 도착
if (graph[i][j] == 1) {
find(i, j);
}
}
}
for (int i = 1; i < n+1; i++) {
for (int j = 1; j < n+1; j++) {
System.out.printf("%d ", graph[i][j]);
}
System.out.println();
}
}
public static void find(int x, int y) {
if (visited[x][y] == true) return;
visited[x][y] = true;
for (int i = 1; i < n+1; i++) {
if (graph[y][i] == 1) {
graph[x][i] = 1;
find(x, i);
}
}
}
}
풀이 회고
해당 문제는 풀다 보니 DFS를 통해 해결 할 수 있었다. 우선 문제에서 요구하는 것은 인접행렬이 주어졌을 때 i에서 j로 가는 경로의 존재 유무이며 각각의 경우에 대해 이를 나타낸 인접행렬을 구하는(출력하는) 것이다. 문제에서 주어진 입출력 예시에 대한 노드간 인접행렬을 그림으로 나타내면 다음과 같다.

첫 번째로 노드가 3개일 때를 보면 "노드 1 → 노드 2 → 노드 3 → 노드 1"로 일종의 사이클이 형성된 것을 볼 수 있다. 결론적으로 노드 1에서는 노드 2와 노드 3뿐만 아니라 자기 자신인 노드 1로 돌아갈 수 있는 경로도 존재하는 것이다. 나머지 노드 2와 노드 3도 마찬가지이다.
두 번째는 위의 예시 보다는 다소 복잡하지만 i에서 j로 가는 간선을 나타내보면 어떤 노드들끼리는 첫 번째 예시처럼 사이클을 형성하는 것도 있고 그렇지 않은 노드들도 있다.
어찌됐든 주어지는 인접행렬에 따라 노드간의 연결은 짧을 수도 있고 길 수도 있다. 이때 노드간의 최소 연결 개수는 아에 연결되지 않은 경우인 0개이며, 노드간의 최대 연결 개수는 주어진 노드 개수 N일 것이다.
이 문제를 해결하기 위해서 생각한 방법은 다음과 같다.
1. 특정 노드와 연결된 노드를 찾는다.
2. 찾은 노드와 연결된 노드를 다시 찾는다.
두 번째 예시에서 1번 노드를 기준으로 위 방법을 적용해보면 다음과 같다.
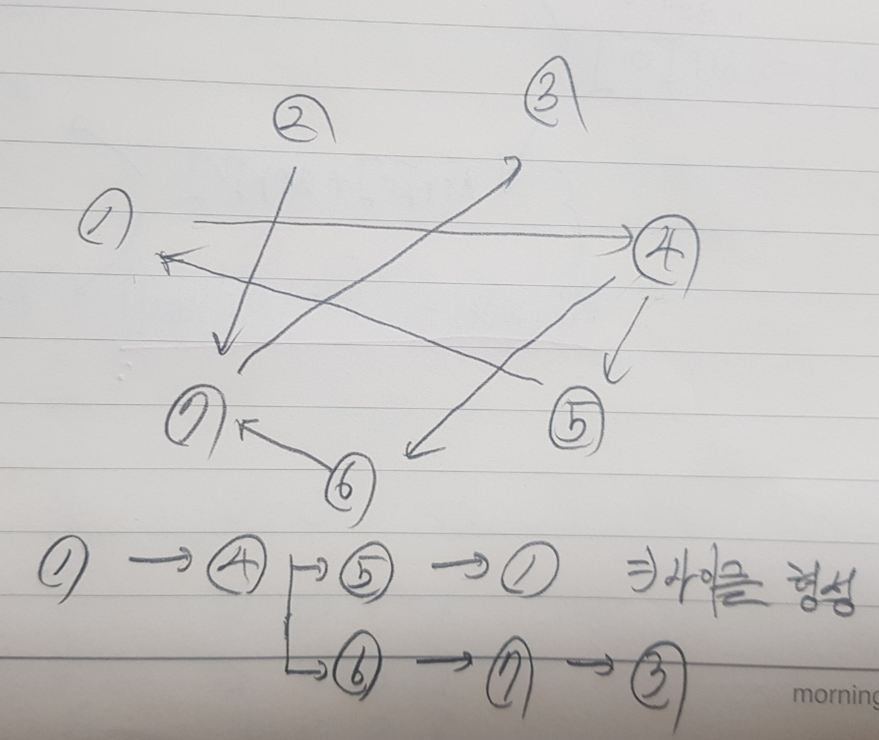
노드 1과 바로 연결된 노드 그리고 이어서 쭉 연결된 모든 노드들은 노드 1에서 출발하여 방문할 수 있는 노드들에 해당된다. 이런 식으로 노드 1 ~ N 순으로 각각의 연결된 노드들을 방문하면서 1로 표기하면 문제에서 요구하는 i에서 j로 가는 경로의 존재 유무를 나타내는 인접행렬을 구할 수 있게 된다.
노드 1 ~ N 순으로 각각의 연결된 노드들을 방문하는 로직은 다음과 같다.
for (int i = 1; i < n+1; i++) { // 기준 노드
for (int j = 1; j < n+1; j++) { // 연결 노드
if (graph[i][j] == 1) {
find(i, j);
}
}
}
하지만 위 코드에서 바로 연결된 노드를 체크만할 뿐이다. 애초에 바로 연결된 노드는 문제의 입력 예시로 1로 표기되어 있기 때문에 별도 작업은 할 필요가 없다. 그 이후에 이어서 연결된 노드들은 위에 뜬끔없이 나온 find 함수를 통해 처리할 수 있다.
public static void find(int x, int y) {
if (visited[x][y] == true) return;
visited[x][y] = true;
for (int i = 1; i < n+1; i++) {
if (graph[y][i] == 1) {
graph[x][i] = 1;
find(x, i);
}
}
}
find 함수는 파라미터로 기준 노드(int x)와 바로 연결된 노드(int y)의 index를 받는다. 이때 연결된 노드를 다시 기준 노드로 두고 이 노드와 연결된 노드를 반복적으로 찾아 가는 것이다. 이를 구현하기 위해서는 find 함수를 재귀 호출해야만 한다.
이때 연결된 노드의 끝이 있다면 재귀 함수는 종료되겠지만(graph[y][y] == 1 조건 미충족) 만약 노드들간의 사이클이 존재한다면 이 재귀함수는 연결된 노드들을 돌고 돌아 무한히 호출될 것이다. 이에 대한 재귀 함수의 종료 조건을 위해 기준 노드 index x와 연결 노드 index y에 대해 방문 처리(visited)를 하면서 방문했었던 적이 있으면 return되도록 했다.
참고자료
- https://www.acmicpc.net/problem/11403
'Algorithm > BOJ' 카테고리의 다른 글
| [백준 - 2512] 예산 - Java (0) | 2022.03.08 |
|---|---|
| [백준 - 10815] 숫자 카드 - Java (2) | 2022.03.08 |
| [백준 - 1149] RGB 거리 - Java (0) | 2022.02.22 |
| [백준 - 1182] 부분수열의 합 - Java (0) | 2022.02.20 |
| [백준 - 2839] 설탕배달 - Java (0) | 2022.02.15 |